The pulling force calculation is based on elementary finite difference calculation of the pull force required to install the individual pipeline segments from entry point to exit point of the pipeline in the reamed hole. The total pull force required to install the pipe is determined by summing the individual forces required to pull the pipe through each of the straight and curved sections defined in the “drilling hole profile” above.
The required pull force for pulling the pipe string is calculated as the force required to overcome combined effects of the following:
- Frictional force
- Drag force
- Force due to change in elevation (potential) of pipe section
The pull force required to pull the pipe through each of the straight and curved sections is calculated as per the following formula:
Straight Section
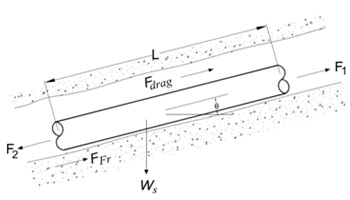
Fig. Free body diagram for pulling of straight pipe section
For any straight section, the pulling force (
F2) is calculated from static force balance as follows:
F2 = F1 + | FFr | + Fdrag ± FP
Curved Section
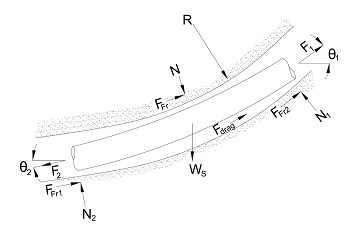
Fig. Free body diagram for pulling of curved pipe section
For any curved section, the pulling force (
F2) is calculated from static force balance as follows:
F2 = F1 + 2 | FFr | + Fdrag ± FP
Where,
| F1 |
= |
Force resisting the movement of the remaining pipe at Point 1
(Summation of forces required to pull the pipe on the left side) |
| FFr |
= |
Frictional force between the pipe and the soil/ rollers |
| Fdrag |
= |
Drag force of bentonite acting on pipe |
| FP |
= |
Force due to change in elevation (potential) of pipe section
(It is negative when the pipe is pulled down the drilled hole and positive when the pipe is pulled up the drilled hole) |